复相关系数

复相关系数是度量复相关程度的指标，它可利用单相关系数和偏相关系数求得。 复相关系数越大，表明要素或变量之间的线性相关程度越密切。

复相关系数法

某个评价指标的复相关系数越大，表示它越能被其他评价指标所替代，它在综合评价中所起的作用就越小。 根据各评价指标的复相关系数，以其倒数归一化作为权重，为多指标综合评价提供依据。

计算步骤

给定$n$个评价对象的$m$个规范化的指标值$X_1,X_2,\cdots,X_m$， 其中$X_i={x_{i1},x_{i2},\cdots,x_{in}}$， 那么$X_i$的复相关系数使用以下步骤计算得到：

Step 1. 使用$X_i$对$X_1,X_2,\cdots,X_{i-1},X_{i+1},\cdots,X_m$做回归，得到

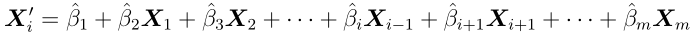
Step 2. 计算$X_i$和$\hat{X}_i$的简单相关系数，或称皮尔逊相关系数(Pearson Correlation Cofficient)

\begin{equation} \rho (\bm{X}_i,\bm{X}_i') = \frac{\sum (\bm{X}_i - \overline{\bm{X}_i})(\bm{X}_i' - \overline{\bm{X}_i'})}{\sqrt{\sum (\bm{X}_i - \overline{\bm{X}_i})^2} \sqrt{\sum(\bm{X}_i' - \overline{\bm{X}_i'})^2}} \end{equation}

$\rho (X_i,X_i')$就是$X_i$与$X_1,X_2,\cdots,X_{i-1},X_{i+1},\cdots,X_m$的复相关系数。

Step 3. 将复相关系数的倒数做归一化处理，记$r_i=\rho (\bm{X}_i,\bm{X}_i')$，$\overline{r}_i = \frac{1}{r_i}$，得到各评价指标的权重

\begin{equation} w_i = \frac{\overline{r}_i}{\sum \overline{r_j}}, i=1,2,\cdots,m \end{equation}

这样就得到了归一化的各个评价指标的权重$\bm{w}=(w_1,w_2,\cdots,w_m)$。