基本思路

拉开档次法是一种体现被评价对象之间整体差异的客观评价方法，该方法的基本思路是选择指标权系数，使得各被评价对象之间的 差异尽可能拉大。从几何角度来看，是将由$m$个评价指标构成的$m$维评价空间中的$n$个点(评价目标)向某一维空间做投影， 使得各点在此一维空间上的投影点最为分散，即分散程度最大。

计算步骤

记评价对象的综合评价函数为下式

\begin{equation} y=w_1x_1+w_2x_2+\cdots+w_mx_m=\bm{w} \bm{x} \end{equation} 其中$\bm{w}=(w_1,w_2,\cdots,w_m)$为$m$维待定正向量，也即权向量；$\bm{x}=(x_1,x_2,\cdots,x_m)^T$是规范化后的评价对象状态向量，也即各个评价指标规范化后构成的向量。

对于$n$个评价对象中的第$j$个评价对象的$m$个观测值$x_{1j},x_{2j},\cdots,x_{mj}$， 将其代入上式，得到

\begin{equation} y_j=w_1x_{1j}+w_2x_{2j}+\cdots+w_mx_{mj}, j=1,2,\cdots,n \end{equation}

若记

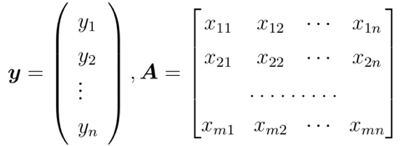
那么可以记作

\begin{equation} \bm{y}=(\bm{wA})^T \end{equation}

根据拉开档次法的基本思路，权向量$\bm{w}$的确定准则是最大化各评价对象之间的差异， 也即，求向量$\bm{x}$的线性函数$f(\bm{x})=\bm{wx}$，使$n$个评价对象此函数取值的方差最大。

根据方差公式$D[X]=E[X^2]-(E[X])^2$，$n$个评价对象的$\bm{y}=\bm{wx}$取值的方差为

\begin{equation} S^2=\frac{1}{n}\sum_{i=1}^n y_i^2 - (\sum_{i=1}^n \frac{y_i}{n})^2=\frac{\bm{y}^T\bm{y}}{n}-\overline{y}^2 \end{equation}

其中向量$\bm{y}$各分量的均值记作$\overline{y}$。

上式的最大值表示为 \begin{equation} \max S^2 = \max \frac{\bm{y}^T\bm{y}}{n}-\overline{y}^2 \end{equation}

对于规范化的决策矩阵

\begin{equation} \max S^2 = \max (\frac{\bm{y}^T\bm{y}}{n}-\overline{y}^2) \approx{\max \frac{\bm{y}^T\bm{y}}{n}}=\max \bm{y}^T\bm{y} \end{equation}

而

\begin{equation} \bm{y}^T\bm{y} = ((\bm{wA})^T)^T (\bm{wA}^T) = \bm{wAA}^T \bm{w}^T = \bm{wHw}^T \end{equation}

其中，$\bm{H}=\bm{AA}^T$。所以

\begin{equation} \max S^2 = \bm{wHw}^T \end{equation}

限定$\bm{ww}^T=1$，上式有最大值，从而问题变为确定权向量$\bm{w}$，使得

$$ \begin{array}{l} \max & \bm{wHw}^T \\ \mathrm{s.t.} & \bm{ww}^T=1 \\ & \bm{w} > 0 \end{array} $$

计算$\bm{H}$的最大特征值所对应的标准特征向量$\bm{w}$，使得$S^2=\bm{wHw}^T$取得最大值。 最后对$\bm{w}$进行归一化，得到拉开档次法计算所得的各个评价指标对应的权重向量

$$ \overline{\bm{w}}=(\overline{w}_1,\overline{w}_2,\cdots,\overline{w}_m). $$